为了通过数值方法近似求解化学主方程,研究者已经做出了许多努力。其中最常用的方法是Gillespie算法。Gillespie算法属于动力学蒙特卡罗方法,可以从所有可能的状态轨迹中采样以生成相关变量的统计数据。然而,为了获得高精度的联合概率分布数据需要进行大量的轨迹模拟,系统的动力学可能会受到罕见但重要的轨迹的显著影响,而这些轨迹很难通过Gillespie算法进行采样。为了改善这些问题,研究者提出了很多改进,例如Gillespie算法的连续版本(化学Langevin方程)、对CME的状态空间进行截断、Finite state projection以及ACME等方法等。然而当物种的分子数有很大波动,或者种类数和分子数都很大时,这些方法仍然具有高计算成本和低计算精度的问题。尽管在这一方面已经付出了很大的努力,目前仍然缺乏一种通过直接表示联合概率分布演化的方式来求解化学主方程的通用方法。
近日,中科院理论物理所彭桓武青年访问科学家、北京师范大学复杂系统国际科学中心的汤迎副研究员和学生翁佳钰与中国科学院理论物理研究所的张潘研究员合作,在Nature Machine Intelligence发表论文“Neural-network solutions to stochastic reaction networks”,提出了使用变分自回归网络来求解化学主方程的机器学习方法,提出用变分自回归神经网络(VAN)[1] 来研究随机反应网络中物种分子数的联合概率分布,刻画联合分布演化并求解化学主方程(图 1)。VAN是张潘研究员与合作者于2019年提出的神经网络变分方法,能够对统计物理微观构型进行有效采样,并计算不同构型的归一化概率,已被应用于统计物理学、量子多体系统、开放量子系统、量子电路和计算生物学。这项工作扩展了VAN以表征随机反应网络中物种分子数的联合概率分布。作为VAN的神经网络单元,作者采用了递归神经网络(RNN)和Transformer架构,它们可以灵活地表示高维概率分布并灵活调整物种分子数的上限。拓展的VAN也允许对每个物种添加物种分子数上限的约束,或者维持某些系统中物种分子总数守恒的约束,这都可以收缩概率空间以提高计算的准确性。新方法采用强化学习框架中的策略梯度算法训练自回归网络,不需要使用其他方法先验模拟的任何数据,给出了一个自动归一化分布作为任意有限时间内化学主方程的解,得到随时间演化的联合分布,提供了高维状态空间中每种构型在不同时刻的概率。此外,此方法在表示多峰分布方面表现出可塑性,对于物种分子数守恒的系统,具有随时间变化的反应速率的系统和高维系统均是非常有效的。
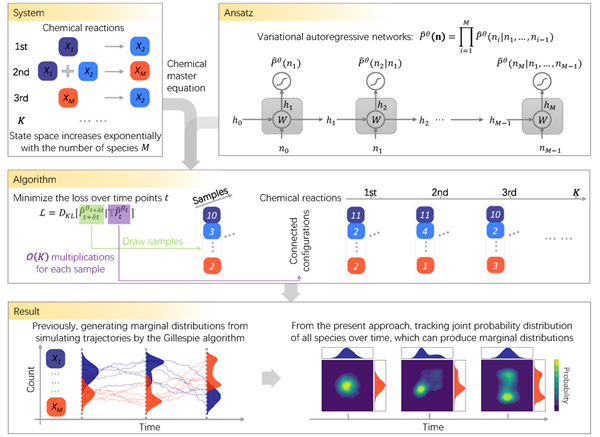
图1:跟踪随机反应网络随时间变化的联合概率分布。(上)对于反应网络,状态空间随物种的种类数增多呈指数级增长,使得跟踪联合分布的时间演化变得困难。变分自回归方法(VAN)可以参数化表示联合分布。(中)从初始分布出发,通过连续时间步长的联合分布之间的KL散度来最小化损失函数,以学习其时间演化。为了在下一时刻训练VAN,从上一时刻分布中抽取样本。每个样本都由一列堆叠的正方形表示,其颜色代表物种,数字表示它们的分子数。对于每个样本,连接构型的数量与化学反应的数量相等。(下)用Gillespie算法模拟轨迹可以产生边际分布,但一般不能准确产生高维联合分布,而VAN跟踪了所有物种数随时间变化的联合分布。
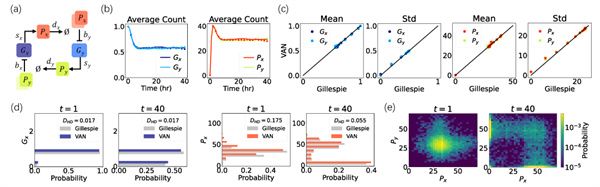
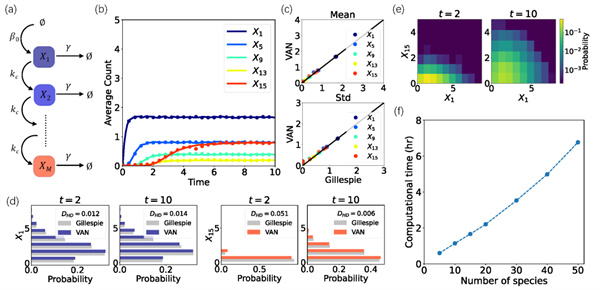
作者将该方法应用于物理学和生物学中的代表性示例,具体的应用包括基因切换开关、细胞内信号级联反应、早期生命自我复制以及具有时变速率的流行病模型等,结果(见图2和图3)证明该方法是一种基于现代机器学习研究随机反应网络的通用方法。
论文链接:
https://www.nature.com/articles/s42256-023-00632-6
论文免费只读版本:
https://rdcu.be/c7MVp
程序包:
https://github.com/jamestang23/NNCME








