然而经典的张量网络缩并方法,例如张量重整化群方法,通常假设系统定义在格点之上。但对于具有不规则连接的张量网络并没有成熟的缩并方法,其中的困难在于缩并过程中会遇到维度巨大的中间张量,却没有很有效的方法对其进行低维近似。这限制了张量网络方法在更广泛的的物理问题中的应用。
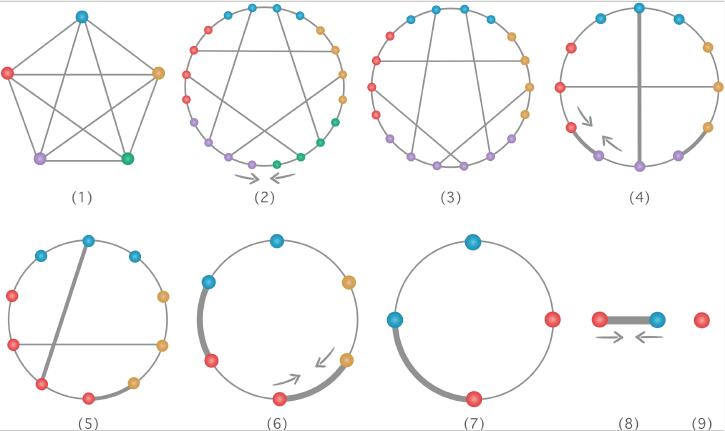
理论物理所研究员张潘和博士生潘峰,周鹏飞,李素洁提出了一种新的张量网络缩并方法,利用矩阵乘积态表述张量网络缩并中所产生的中间张量,并用密度矩阵重整化群进行有效的近似,压缩中间张量的维度,进而可以对任意张量网络进行缩并。下图是新方法对由5个4阶张量所组成的张量网络进行缩并的示意图:(1)中每个4阶张量被表示成(2)中的一个矩阵乘积态(MPS),然后不同MPS合并成更长的MPS,并采用低秩近似降低它们的维度,最后得到(9)中的缩并结果。新方法在统计物理自由能计算方面展现出强大的能力,在多种拓扑连接结构的自旋玻璃自由能计算问题中相比传统方法具有更高的计算精度和更快的计算速度。另外新方法可以以较小的计算误差对浅层量子线路进行经典模拟,具有模拟和验证含噪声的中型(NISQ)量子计算机的潜力。
该研究工作得到了国家自然科学基金委面上项目和中科院前沿科学重点研究项目的支持。
文章链接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.060503








